N-Body simulations

While I observed the bright, rich globular clusters M15 and M2 in autumn 2011, I wondered how the trajectories of  stellar members  might look in such a million body system.  I assumed a somehow chaotic appearance. Not quite sure, I decided to make computer models for such systems to gain some insight.
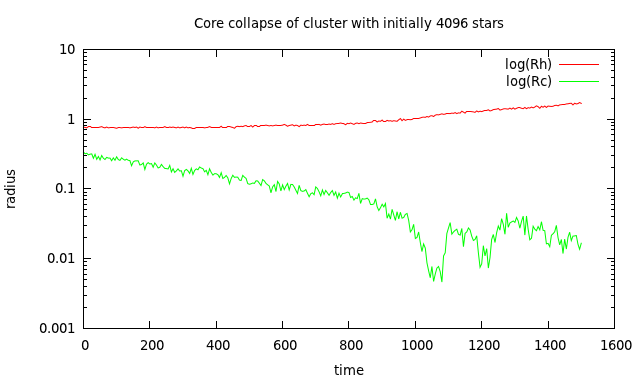
The ~150 globular clusters in our Galaxy are among the oldest objects known. How could they survive as stable objects over times of more than 12 billion years?  I previously had read about a core collapse and a black hole in the center of M15, but I was suprised to read what a complex system such a cluster is. Read: A Thousand Blazing Suns: The Inner Life of Globular Clusters.

Other galaxies have globular clusters as well. With a midrange Dobsonian it is possible to observe the brightest in M31, the nearby Andromeda Galaxy. One of the most impressive images I have seen yet, is from William E. Harris' website. About 16000 globular clusters in the halo of giant elliptical galaxy NGC 3311, the centrally dominant cD galaxy in the Hydra I cluster.

 

Following the evolution of such a system means to integrate directly the N individual equations of motion, this is the N-body approach.
It is not advisable to start this numerical work from scratch, using Runge-Kutta integrators or something comparable. It took decades to develop state of the art methods, used in special software like NBODY4, NBODY6 or the starlab-code which is used here.

Although a real globular cluster has about ten to hundred times more stars than the modells below, you will get an impression about the dynamics. It might be interesting to note, that clusters of a million members, consisting of a realistic fraction of binaries are still beyond reach of current computer power. Special treatment is used for close encounters and binary or multiple subsystems that form either dynamically or exist in the initial configuration.



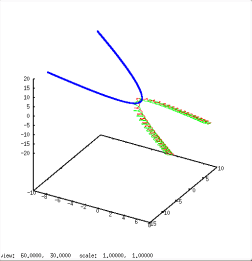
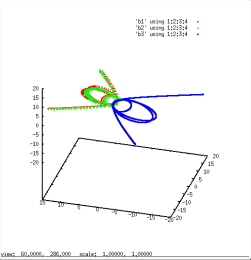
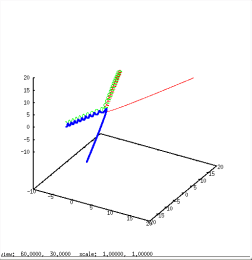
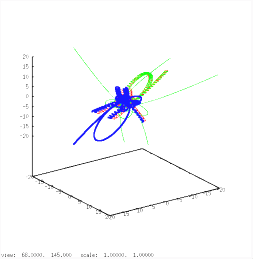
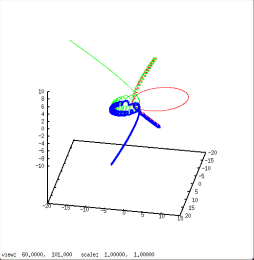
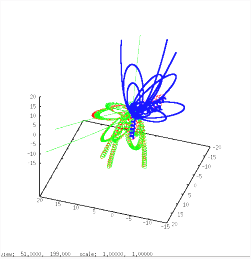
Six examples of three body encounters. In all cases a binary (m1=0.55, red and m2=0.45, green)  and a field star (M=0.77, blue) interact in a more or less complicated way. In the first and second case the configuration is preserved. In all other cases the original binary is disrupted and  the light m2 component (green) escapes. With a  gain in  kinetic energy=velocity it often leaves the cluster. Frequency of close interactions is highest in dense regions. The rearrangement of energies among the participants in many cases enables the binary to leave the core also. This is a mechanism to delay, prevent or reverse a core-collaps (see below).

If such an exchange process happens in the cluster's core, chances are good, that a fresh formed couple consists of a  main-sequence star and a heavy, compact object like a white dwarf or a neutron star, which dominate the stellar population in this region.  The dynamical interaction between the partners, mass transfer in close binary systems causing enforced stellar evolution ..., enriches the core region with all sorts of relativistic binaries.
 
Stellar and binary evolution, concentration of massive stars in the core, stellar collisions in crowded regions, possible presence of a central black hole and the tidal field of the Galaxy must also be considered, when the model should give a realistic match to an existing globular.

The following videos are best viewed in full screen mode.  Works with Firefox  and Chrome, Internet-Explorer will  offer a download ...

A small globular cluster:  King W12, 1024 bodies, t=0..10

These simulations were made with the KIRA-Integrator available for download from the Starlab site.

It is quite easy to use the Starlab tools to make simple things:

and really complicatet things:

Create a King model with a power-law mass spectrum and a binary population, then evolve it with stellar and binary evolution. Use all 4  CPUs for integration

 makeking -n 5000 -w 7 -i -u \
	| makemass -f 1 -x -2.0 -l 0.1 -u 20 \
	| makesecondary -f 0.1 -l 0.1 \
	| add_star -Q 0.5 -R 5 \
	| scale -M 1 -E -0.25 -Q 0.5 \
	| makebinary -f 1 -l 1 -u 1000 -o 2 \
	| kira -T 4 -t 100 -d 1 -D 10 -f 0.3 \
                      -n 10 -q 0.5 -Q -G 2 -B

Almost all commands display detailed help for their usage. Try: 

makeking --help
or
kira --help

Unfortunately starlab does not make use of the spectacular power of todays gpgpu-computing. To benefit from recent developments, I have to switch to another package: NBODY6.
Modern graphics processing units (GPUs) can speed up computations by more than 100 times.

The above shown examples represent the state with beginning of 2012. Meanwhile it is February and I purchased a Nvidia GeForce GTX460 GPU to speed things up.
It now takes 31 seconds instead of 2 hours to compute the above results.
Below is a first core collapse of a cluster shown, computed with nbody6.gpu, the code provided by Sverre Aarseth's Institute of Astronomy N-Body and Downloads Page

The achieved GFLPOS depend on the number of particles in the system. In NBODY6 it goes asymptotically to ca. 500 GFLOPS when N > 50000.
Later I found, that best perfomance of the GTX460 results, when the number of stars is choosen such that N=7 x 2**k.
Measurements were made with help of the nbody-code from the NVIDIA-GPU-Computing-SDK.

Core Collapse

It took about a hour to compute the result below. Starting model was a Plummer sphere  of equal mass stars, computed with:
  

 mcluster -P0 -N 4096 -f 0 -t 0 -O 5.0 -T 1500.0 -C 0 -G 1 -u 0

The mcluster code is developed by Andreas Küpper :  http://www.astro.uni-bonn.de/~akuepper/mcluster/mcluster.html
Without this code you will hardly have a chance to generate desired NBODY6 input files.
Documentation of NBODY6 is out of date and you need the remembering brain of an elephant to manage the combinations of ~100 parameters (numbers) that drive the computations.

This new state-of-the-art 3D-technology is known as X3DOM and requires latest browser versions. Best results are obtained with google chrome vers. 17  or higher.

If you plan to fly through the cluster, Firefox (Version < 11) is currently not a responsive  space ship.

More about N-body computations and detailed explanations:

Books:

The Cambridge N-Body lectures

The Gravitational Million-Body Problem

Sites:

www.nbodylab.org
www.manybody.org
www.artcompsci.org
www.nbodylab.com
www.sverre.com the home of nbody6.
www.amusecode.org


Also detailed explanations  in Wikipedia.