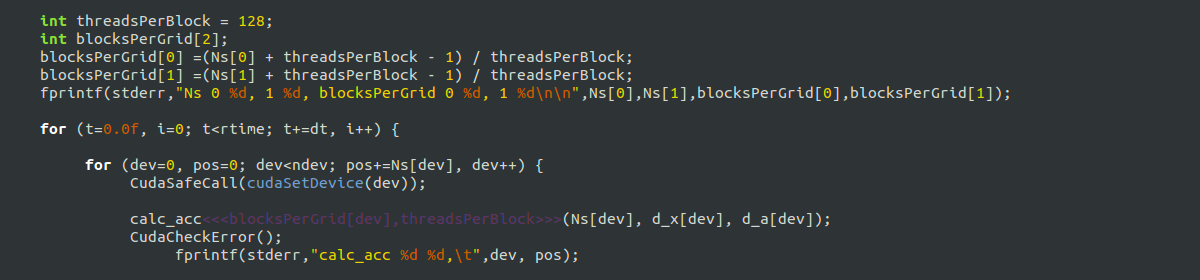
Wer sich einbildet, am Himmel schon alles gesehen zu haben, wird hin und wieder doch noch überrascht, so wie ich, bei diesem Prachtexemplar.

Gut, wer kennt sich schon am Südhimmel so gut aus …
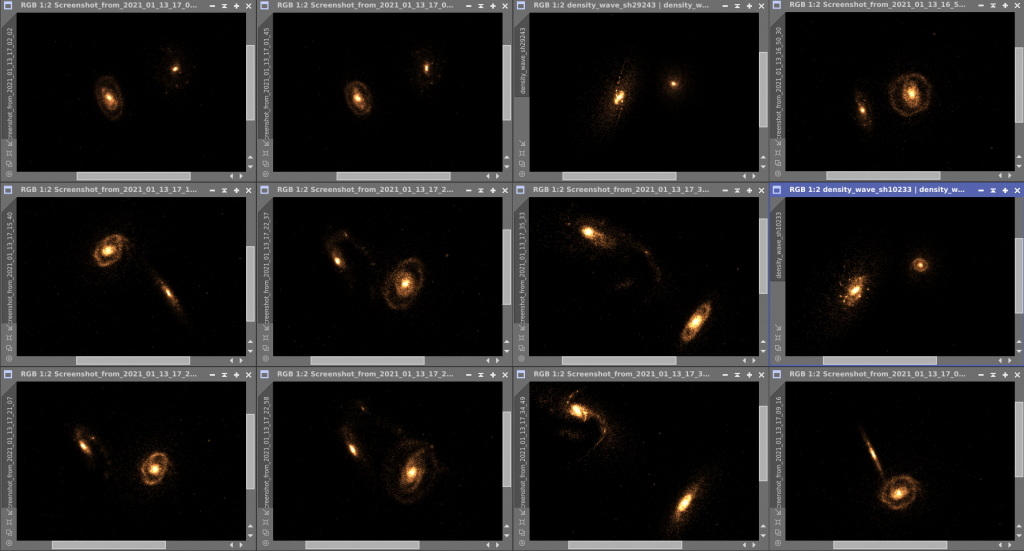
Hier zunächst ein Sammlung von sechs zufällig ausgewählten Galaxien des Originalkatalogs. Alle Bilder wurden mit dem Hubble Space Telescope gemacht.
Ich will im folgenden eine Kollektion von selbstgemachten “Arp-Galaxien” zeigen, die der liebe Gott auch nicht schöner gemacht hätte, vielleicht etwas bunter. Sie entstanden bei dem Versuch, die Entstehung der Cartwheel Galaxie zu simulieren.
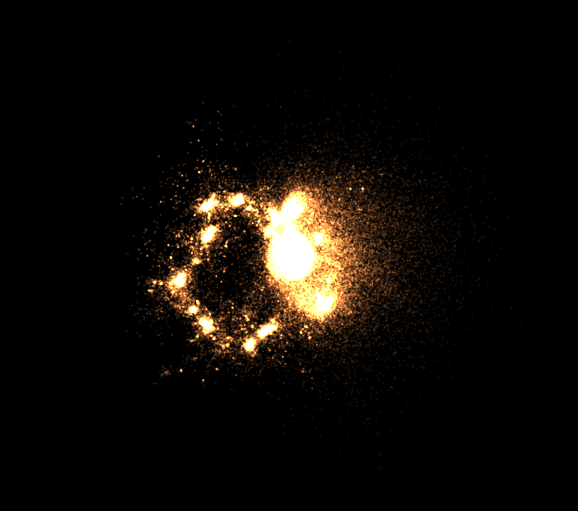


Ich erzähle dazu noch etwas interessantes über N-Body Simulationen. Es ist nämlich so, dass wir hier bei diesen Galaxien-Crashs deutlich schneller als in Echtzeit rechnen können. 🙂
Wenn der Computer z.B. für die Herstellung der Filme im vorhergehenden Beitrag zu Arp 271, ca. 2 Minuten für 80000 Sterne brauchte, wie lange rechnet er dann am wirklichen Problem von 200 Milliarden Sternen?
Nun, die Rechenzeit ergibt sich zu
t2 = t1 * N2 * log(N2) / (N1 * log(N1))
das sind also
t2 = 650 * 10**6 Sekunden = 22 Jahre.
Warum rechne ich solch einen Quatsch hier vor? Na ja, es wird den Einen oder Anderen erstaunen, wenn ich sage, dass man mit dem schnellsten Computer der Welt keinen Kugelsternhaufen von 1 Million Sternen in seiner dynamischen Entwicklung durchrechnen kann! Nicht in 1000 Jahren.
Mmmh, wer 200 Milliarden auf der Bank hat, kann sich doch deutlich weniger Sorgen machen als der einfache Millionär. Wie im wirklichen Leben sind das zwei Paar Schuhe.
Im Fall der Galaxien sind die physikalisch/astronomischen Gegebenheiten im Vergleich zu den Kugelsternhaufen deutlich entspannter. Für die Dynamik des Galaxiensystems ist es völlig unerheblich, wenn sich im Verlauf der Kollision eine Handvoll Sterne ziemlich nahe kommen oder gar zusammenstoßen. Wurscht, die Galaxie ist einfach zu groß. Numerisch firmiert das ganze unter “collisionless N-body simulation”. Man nutzt in der Berechnung der Kräfte eine “softening”-Parameter, der auch im Computer alles im grünen Bereich hält, wenn sich zwei Sterne ziemlich nahe kommen.
Im Kugelsternhaufen ist das was anderes. “Collisional N-body” muß alle Vorkommenden Abartigkeiten durchrechnen. Wer also 12 Milliarden Jahre Entwicklung rechnen will und dabei gezwungen ist, z.B. die enge Begegnung zweier Neutronensterne im Millisekundenbereich durchzurechnen, der hat zu tun. Das muß man machen, denn sonst kommt schnell ein völlig anderes Ergebnis heraus! Der Kugelsternhaufen reagiert sehr empfindlich. Es gibt auch hier sehr, sehr raffinierte Rechenmethoden, aber trotzdem gilt das oben gesagte. Die Rechenzeit wächst hier proportional mit N*N !
Nach dem letzten Beitrag wurde die Frage gestellt, ob das Resultat der Verschmelzung ein elliptische Galaxie sein wird? Ja, das ist die Lehrmeinung und es ist auch im unten folgenden Video zu sehen. Die Galaxien hier umrunden sich zunächst, zerfetzen sich und bilden dabei lange Schwänze aus, wie sie von der Antennen- oder der Tadpole-Galaxie bekannt sind.


Etwas amateurhaft, dafür diesesmal in OpenGL. Sieht so etwas realistischer aus. Es ist immer derselbe Crash nur oft geschnitten, damit es nicht zu langweilig wird. Die Galaxien durchdringen sich dabei zweimal, bevor sie entgültig verschmelzen.
Zunächst denkt man: “Da tut sich nicht viel …”
Aber dann: “Begeistert sein …”
Wer es genau wissen will, wie das mit den N-Body Problemen ist: