Und? Kannst du mir beipflichten:
Das Universum ist bösartig, Optik ist schlimmer, Microsoft toppt alles !
Nein? Dann bist du entweder
– kein Amateurastronom in Deutschland,
– hast den Uwe Laux nicht im Regal stehen
– und/oder hast nie einen Windows-PC in deiner Sternwarte betrieben …
Wer je ein Buch über Optik in die Hand nahm, erwischte mit Sicherheit ein ganz, ganz schlechtes. Es gibt mehr davon als Sand am Meer. Schlagt mal eins auf, ihr kommt aus dem Staunen nicht mehr raus vor lauter Fachchinesisch.
Transversal, sagital, meridional, tangential, marginal, … scheissegal, zack und das Buch fliegt in die Ecke. Nach drei Wiederholungen landet es im Regal, ganz oben rechts, wo all die anderen Optikbücher verdientermaßen lauern.
Andererseits lieben wir als Amateurastronomen unsere Fernrohre, Kameras, Montierungen … und wollen eigentlich wissen, wie solch ein APO oder RC funktioniert, oder?
Richtig. Dafür gibt es natürlich auch gute Bücher. Den Laux nicht, das hatte ich ja schon erwähnt. Haben aber viele im Regal. Hier kann man nichts lernen, noch nicht einmal was nachschlagen. Unter den vielen Zahlen finden sich immer gerade die nicht, die man braucht. Er trägt deshalb die dickste Staubschicht.
Ach jetzt höre ich ein Aufstöhnen: Ich liebe meinen Laux, ohne den Laux wüßte ich nichts über Astrooptik, in meinem Laux lese ich täglich vor dem Einschlafen … Stopp! Schön für dich.
Ich empfehle für Astrooptik den Rutten & van Venrooij
 ISBN:0-943396-18-2
ISBN:0-943396-18-2
– kann man lesen wie einen Roman und man findet fast alles.
Für Physiker, egal ob studiert, diplomiert, promoviert, habilitiert oder emeritiert, empfehle ich den Hecht. Die 4. Auflage gibt es für unter 15 € im Internet. https://biblio.co.uk/book/optics-4-e-hecht/d/860341576
ISBN : 8131718077
Hier findet ihr den Rest. – Oder sucht mal nach “introduction to lens design pdf”. Hier das Buch der Bücher über Teleskopoptik, das gibt es sogar umsonst zum download:
https://b-ok.cc/book/511653/eaa37e
Leider sind die hier gemachten Empfehlungen alles englische Bücher. Die sind aber meist generell viel besser. Die Autoren bringen die Sache auf den Punkt, ohne sich zu verzetteln und sich mit jedem Detail rumzuschlagen.
Da ihr nicht solange warten wollt, und es in den folgenden 5 Teilen heftig zur Sache gehen wird, erkläre ich hier zwei Diagramme, die immer benutzt werden, um die Qualität einer Optik zu beurteilen.
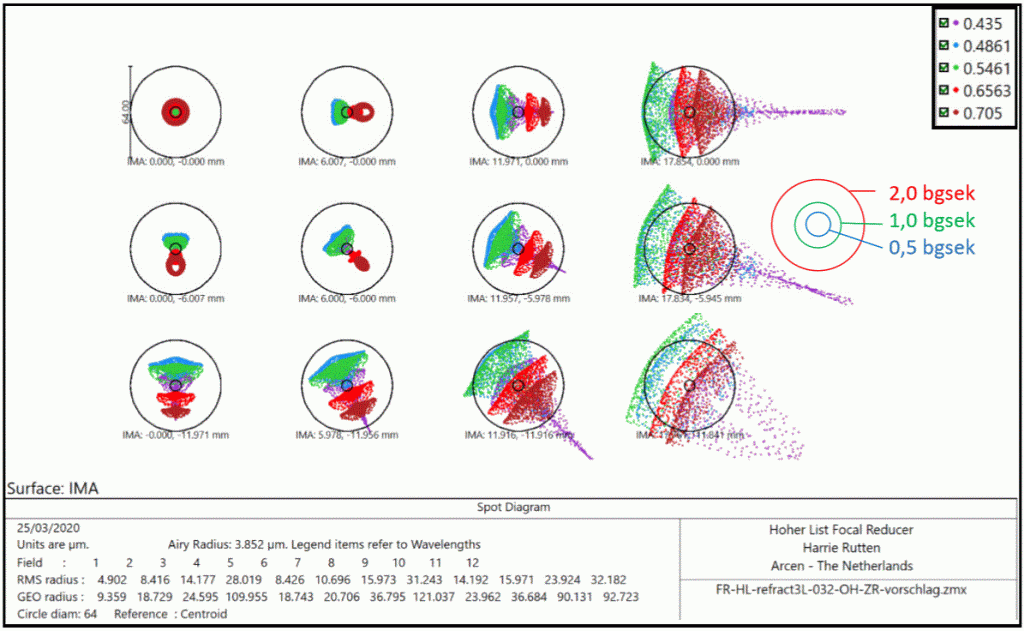
Preisfrage: Wie sieht für den Optiker ein ideales Fernrohr aus? Da gibt es natürlich die Spotdiagramme. Die sind ganz einfach zu verstehen. So sehen die Sterne im Fernrohr aus. Man wünscht sie klein und nadelscharf, bis in die Bildecken. Etwa so:
Hier ist das, was Harrie Rutten uns als Reducer/Korrektor ausgerechnet hat:
Ist das jetzt gut oder nicht? Kommt auf das lokal mögliche Seeing an.
In der Optik muß man immer Kompromisse machen. Bei uns ist es sehr gut, auf dem Cerro Paranal eher nicht.
Wir wollten ja noch das zweite Diagram besprechen, das man immer wieder sieht. Z.B. der Laux ist voll davon. Hier seht ihr also ein ideales Fernrohr:
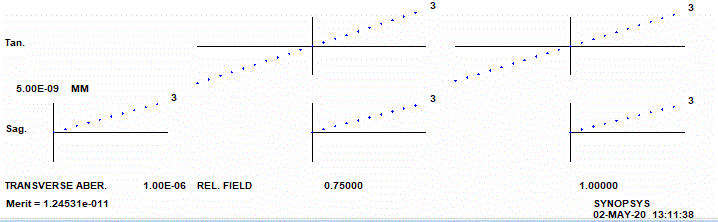
Bild 4: Ideales Fernrohr
Wenn ihr nicht so gute Augen hättet, würdet ihr eigentlich nichts sehen, nur die Koordinatenlinien.
Denn, achtet mal auf den Maßstab! Ganz links im Bild seht ihr den Fokus, wie er entlang der x-Achse von der optischen Achse (Nullpunkt) bis zum Bildfeldrand variiert. Ein ablesbarer y-Wert ist nicht so gut. Also 5 milliardstel Millimeter! Ok, nicht ideal aber …
Dann steht da schon wieder Tan. und Sag. Finden sich schon oben in der Liste. Sie bedeuten folgendes:
Tangential: Man erzeugt im Computer ein Koordinatensystem x,y,z, dessen z-Achse die optische Achse des Systems ist. Sie zeigt aus dem Bildschirm raus, d.h. wir sehen nur auf die x,y-Ebene. Wir erzeugen jetzt einen Fächer von Lichtstrahlen, der von oben bis unten die y-Achse löchert. Die Strahlen laufen also zunächst parallel zur z-Achse und treffen auf die Teleskopöffnung.
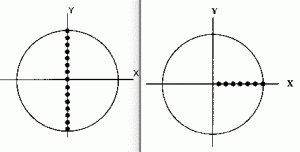
Links im Bild: tangentialer Fächer (tangential ray fan)
Sagital: Der sagitale Fächer läuft nur vom Nullpunkt, entlang der x-Achse bis zum Bildfeldrand.
Was soll das? Nun, die beiden Lichtfächer offenbaren unterschiedliche Probleme. Kommen wir gleich drauf.
Im obigen Bild 4 sehen wir die Optik bei 75% des Bildfeldes in der Mitte von Bild 4 und bei 100% rechts in Bild 4, also am Bildrand. Die y-Achse behält den Maßstab. Laufen die Strahlen parallel zur optischen == z-Achse, so gibt es einen Bildpunkt im Nullpunkt der gezeigten Koordinatenachsen. Wächst dann der Einfallswinkel in der y-z-Ebene so bekommen wir die tangentialen Kurven wie sie im nächsten Bild zu sehen sind. Sie stammen von unserem 1m-Cassegrain.
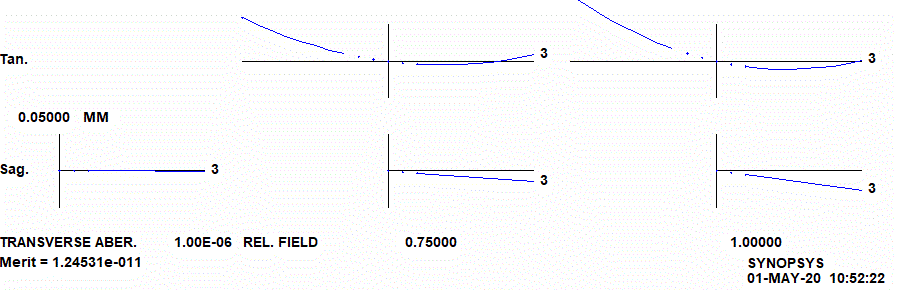
Die Abweichungen in y gehen jetzt bis zu 0.05mm. Oben tangential, unten sagital. Zusammen werden sie als transversale Aberrationen bezeichnet.
Während wir links eine gerade Linie sehen (Gerade, sowas wie y=m*x), zeigen die krummen Kurven sowas wie die Funktion y = a*x^3 + … (x hoch 3). Man spricht hier von Abbildungsfehlern==Aberrationen 3. Ordnung, die auch als Seidelsche Aberrationen bezeichnet werden. Da gibt es die
– sphärische Aberration, auch Öffnungsfehler oder Kugelgestaltsfehler genannt (die Optik macht es einem nicht einfach)
– den Astigmatismus
– die Bildfeldwölbung
– und die Verzeichnung
All diese Probleme lassen sich an den obigen Kurven ablesen.
Wenn ganz links die Linie immer eine Gerade bleibt, egal welchen Winkel sie gegen der x-Achse einnimmt, ist das Teleskop nur defokussiert (harmlos, Problem 1. Ordnung), verschwindet durch Drehen am Okularauszug, scharf wenn auf der x-Achse.

Wenn sich dort eine Kurve zeigt, bekommen wir die nicht glatt auf die x-Achse. Das ist die sphärische Aberration. Sollte bei keinem Fernrohr deutlich sein!

Im folgenden Bild ist noch Koma zu sehen:
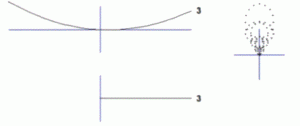
und hier der Astigmatismus:
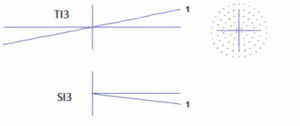
Es gibt eine tangentiale und eine sagitale Komponente. Der Astigmatismus ist die Differenz zwischen den beiden Geraden.
Dazu kommen noch die im folgenden Bild zu sehenden chromatischen Probleme, die auftauchen, wenn das Licht durch Glas hindurch muß.
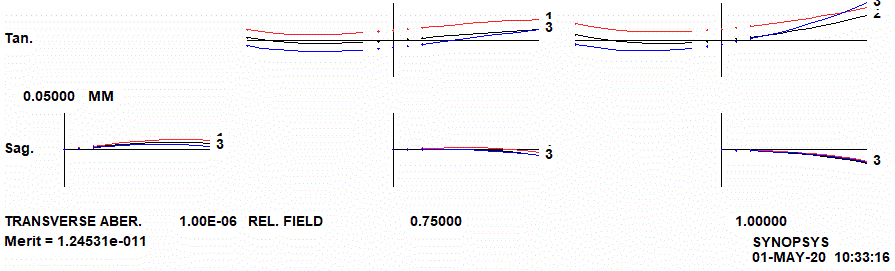
Wir sehen hier den gutartigen Verlauf, wenn wir unser Teleskop mit dem neuen Korrektor bestücken werden.
Zum Schluß noch eine brutal schlechte Optik, um mal die Kurven zu zeigen.
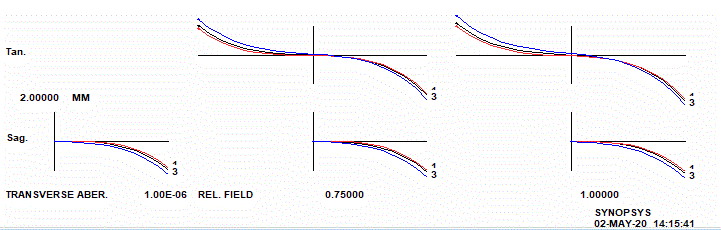
Es folgen fünf weitere Teile …