Wahnsinn Teil 2

 

wir hatten im letzten Beitrag die gleichmäßig beleuchtete Teleskopöffnung fouriertransformiert und das Bild eines Beugungsscheibchens (Psf=Bild des eigendlich punktförmigen Sterns) erhalten, das auf der optischen Achse lag. Die Frage jetzt lautet: Wie bekommt man es an eine beliebige Position ?

Das geht so. Sagen wir die optische Achse gehe durch das Zentrum unseres Koordinatensystems in der Bildebene, und der Stern solle von 0,0 in den Punkt x=0, y=1 überführt werden, dann gelingt uns das, indem wir ein weiteres Bild  gleicher Größe erzeugen, indem alle Pixel auf 0.0 stehen. Alle? Nein ein einzelnes, nämlich 0,1 erhält der Wert 1.0.

Von beiden Bildern, dem mit der Psf, das wir A nennen und dem Neuen mit dem Punkt = Bild B, erzeugen wir gesondert je eine FT.  Da die FT uns in die Welt der komplexen Zahlen zwingt, bekommen wir als Resultat jeweils zwei Bilder geliefert. Eins für den Realteil, eins für den Imaginärteil von a und b.

Die Transformierte der Psf dabei ist gerade die gleichmäßig weiße Eingangsöffnung des Teleskops (Realteil) bzw. ein schwarzes Bild für den Imaginärteil, die FT des Punktes ergibt zwei Wellenbilder ein kosinusförmiges für den Realteil und ein sinusförmiges für den Imaginärteil .

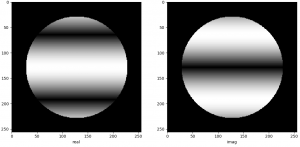
FT wenn Punkt bei 0,1. Der Kreis entsteht durch die Öffnung des Fernrohrs. Leider liegt der Koordinaten-Ursprung in den Beispielbildchen oben links. Sorry!

Im nächsten Schritt führen wird eine sogenannte Faltung der Ergebnisse durch. Das ist im Fourierraum nur eine pixelweise Multiplikation von Real- mit Realbild, von Imaginär- mit Imaginärbild.

Wenn wir das Ergebnis zurücktransformieren, sitzt der Stern an der Stelle 1,0!

Deutlicher wird das bei einer größeren Verschiebung, sagen wir nach 2,11

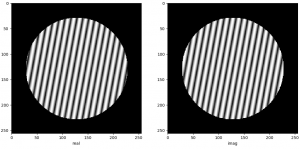
FT wenn Punk (bzw. delta-Funktion) bei 2,11

Wenn wir das Ergebnis zurücktransformieren, sitzt der Stern an der Stelle 2,11!

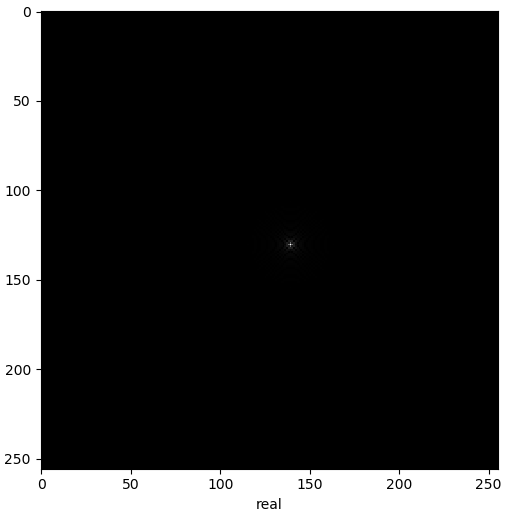
Interessant ist dabei der Anblick des Faltungsbildes. Es zeigt sich, dass die  Wellenlänge und Ausbreitungsrichtung hängen von der gewünschten Punktposition abhängt. Je weiter der Punkt vom Ursprung, desto kürzer die Wellenlänge.

Wenn wir zwei Punkte wählen, gibt es zwei Wellen, die sich überlagern…

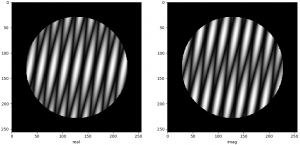
Überlagerungen in der Teleskopöffnung, wenn sich zwei Sterne im Bildfeld befinden.
FT der vorherigen Abbildung.

Die hier beschriebene Methode ist in der Fouriertheorie als Shift-Theorem bekannt.