Beim Aufräumen meiner Festplatten fiel mir ein Powerpoint-Vortrag in die Hände, der eigentlich zu schade ist, um da für ewig zu kreisen. – Anfang 2018 war ich Teilnehmer an einem Extra-Seminar bei Prof. Hans Fahr an der Bonner Uni. Es wurden Vorträge aus verschiedenen Gebieten der Astrophysik gehalten. Meiner lautete: Aperture Synthesis oder wie man mit ALMA Bilder macht.
Ich hatte keine Ahnung vom Thema, obwohl ich es selber ausgesucht hatte.
Immer wenn ich den ESO-Messenger bekomme, finden sich in den Heften viele Bilder die mit dem Atacama Large Millimeter/submillimeter Array (ALMA) gemacht wurden, wie dem folgenden:

Da ist es nicht schön, wenn man nicht weiß wie das im Detail gemacht wird. Im Internet fand ich nur dünne Erklärungsversuche 🙁
Das ist Blöd, denn schließlich arbeitet auch der weltweite Verbund von Radioteleskopen, der das Schwarze Loch in M87 “fotografiert” hat, nach demselben Prinzip wie ALMA.
Laßt euch also nicht länger mit dünnen Erklärungen hinhalten. Ja, es ist etwas kompliziert. Wer aussteigt sollte sich wenigstens die Filme am Ende des zweiten Beitrags ansehen. Es bleibt bestimmt was hängen.
Bei einem komplizierten Thema denke ich oft: Wenn du das programmieren kannst, dann hast du es im wesentlichen verstanden. Somit lautete die Frage:
Kann ich einen Simulator für ALMA programmieren?
Fangen wir aber von vorn an. Hier einige Facts:
ALMA, 66 Parabol-Antennen von meist 12m Durchmesser, liegt im Norden Chiles, in der trockenen Atacama, über 5000m hoch, um dem Wasserdampf zu entgehen. Die 100t schweren Antennen können einzeln versetzt werden, so dass sich ein Radio-Teleskop von bis zu 16km Durchmesser ergibt. Es arbeitet als Interferometer im mm-Wellenlängenbereich und darunter (submillimeter). Man macht damit die zur Zeit schärfesten Bilder. Die Frage ist: Nur wie???
Bilder macht man doch hiermit

8MPix 36MPix 1,5MPix
50° 12° 0.4°

Aber mit den Dingern? Preisfrage: Wieviele Mega-Pixel, welcher Blickwinkel?
Kaum zu glauben, aber hier sieht man es im Detail: 1 Pixel !!!
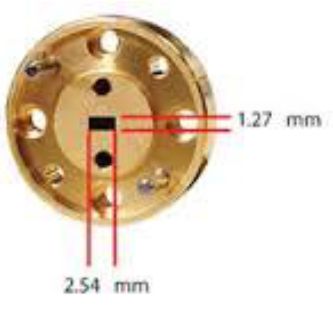
Blickwinkel im Bereich von Bogensekunden.
Na ja, irgendwann waren auch die Radioastronomen zur Einsicht gelangt, dass das ja eigentlich besser gehen müßte. Sie haben verschiedene Pixel für unterschiedliche Wellenlängen (Lochdurchmesser) in der Bildebene kombiniert, wie man im folgenden Bild sieht. Sie sind nach fallenden Wellenlängen durchnummeriert.

Die von der Radiofraktion haben aber auch Vorteile gegenüber der optischen Astronomie: Sie können nicht nur in, sagen wir 1-3 Farben (RGB) gleichzeitig beobachten, sondern in z.B. 256 auf einen Streich. Sie bekommen somit pro Pixel ein kleines Spektrum. Weiterer Vorteil: Sie können die Ankunftszeiten ihrer Signale speichern und sie haben einen größeren Durchlaßbereich in der Atmosphäre und somit auch im Spektrum zur Verfügung
Bevor ich auf die Technik des Interferometers eingehe, zeigen ich hier noch den Radiohimmel und einige seiner hellsten Objekte. Etliche sieht man im optischen kaum!

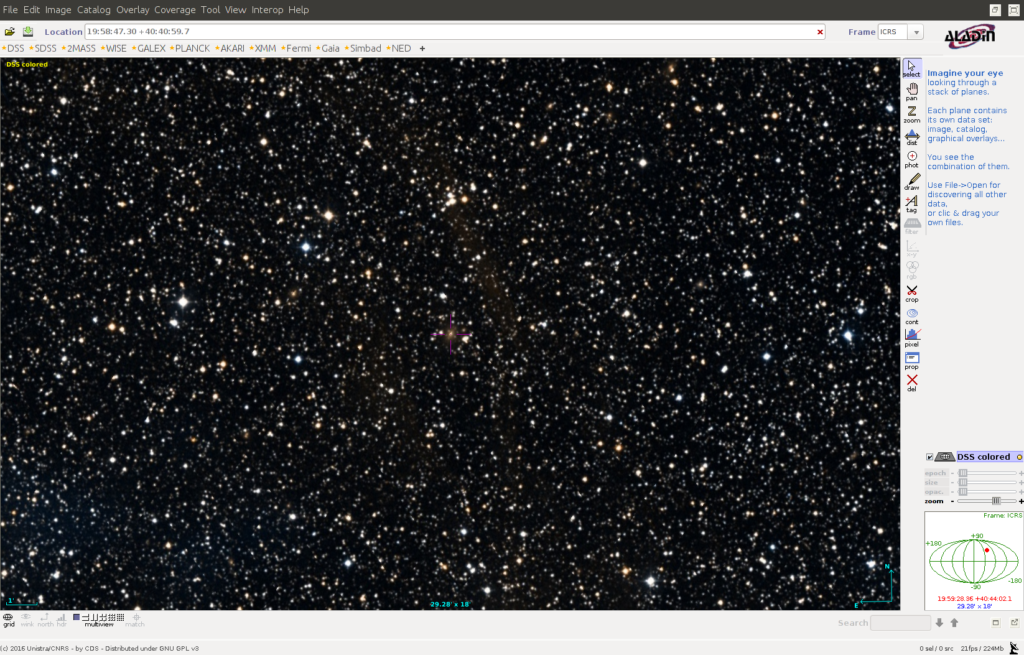
Die Radiostrahlung wird in der verschiedenen Himmelsobjekten auf unterschiedliche Art und Weise erzeugt.
Man unterscheidet Continuum Sources und Spectral Line Sources.
Die ersten Sorte unterteilt sich noch in thermische und nicht-thermische Quellen. Zu den thermischen gehören etwa die 3K-Hintergrundstrahlung, Staubwolken, der Mond. Nicht-thermische Quellen sind z.B. ionisierte Nebel, SNR, Radiogalaxien, M87==Virgo A, 3C273, wobei die letzten 4 Synchrotronstrahlung über Jets aussenden.
Zu den Spectral Line Sources zählen HI-Gebiete (21-cm spin flip), Spektren der Moleküllinien wie H2, CO, Rekombinationslinien und Maser.
Gemessen wird die spektrale Flußdichte in der sehr kleinen Einheit Jansky.
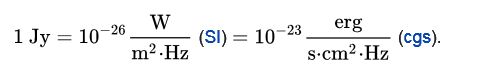
![Radiohelligkeiten in [Jy]](https://giga-parsec.de/wp21/wp-content/uploads/2021/06/stoerer-1024x305.jpg)
___________________________________________
Jetzt wird es etwas trockener, geht aber nicht anders, es wird in Teil 2 gebraucht.
Wer mit einem guten Fernrohr einen Stern bei hoher Vergrößerung betrachtet, sieht keinen Punkt, sondern ein Beugungsscheibchen, das im Schnitt dem Beugungsbild beim Spalt ähnelt.
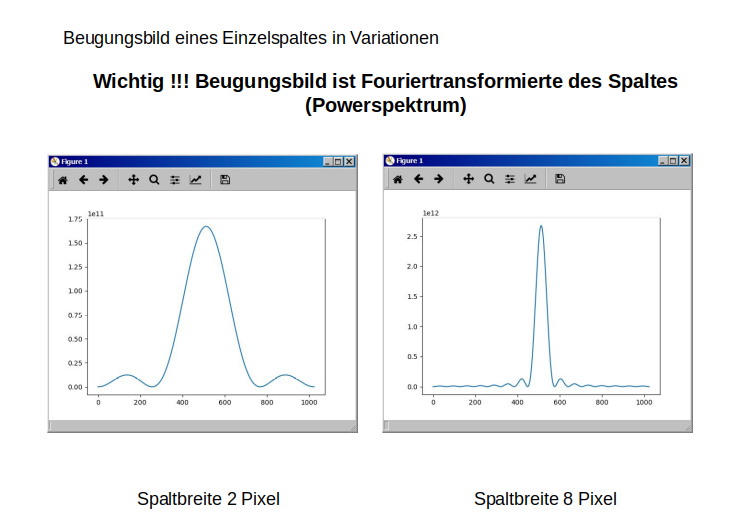
Je kleiner die Öffnung des Telekops, je breiter größer das Beugungsscheibchen und umgekehrt (wie oben beim Spalt). Natürlich geht bei kleineren Teleskopen auch die Höhe der Kurve runter.
Noch ein Einschub, der die ganze folgende Gymnastik rechtfertigen soll.
Das Radioteleskop in Effelsberg hat eine vollbewegliche 100m-Schüssel, es wiegt ca. 3000t. Bei 10cm Wellenläge passen also 1000 Wellenzüge auf den Durchmesser. Wenn man das mit euren optischen Teleskopen vergleicht, sagen wir bei 500nm = 0.000 000 5m, bei 0.2m Öffnung, dann passen hier 400000 Wellenzüge rein. Will sagen: Effelsberg ins optische übertragen hätte eine Öffnung von 0.5mm (Millimeter!!!) . Wer sich solch ein Teleskop gönnt, braucht nicht mal eine Linse, alles wird dann von der Beugung dominiert, darunter leiden die Radioastronomen. Wir können mit der einfachen Strahlenoptik eine ganze Menge erklären.
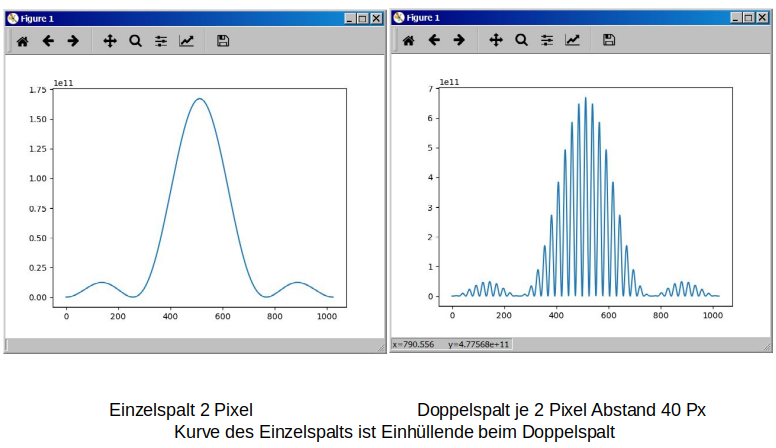
Also weiter mit der Beugung des Lichts. Beim Doppelspalt wird die Kurve des Einzelspalts noch durch ein weiteres Muster überlagert, dessen Frequenz vom Abstand der Spalte bestimmt wird. Je weiter auseinander, desto mehr auf und ab. Das hat Konsequenzen für das Auflösungsvermögen und das ist schon der wesenliche Trick der Interferometrie: Nimm 2 und schieb sie auseinander. Der Rest ist Mathematik.
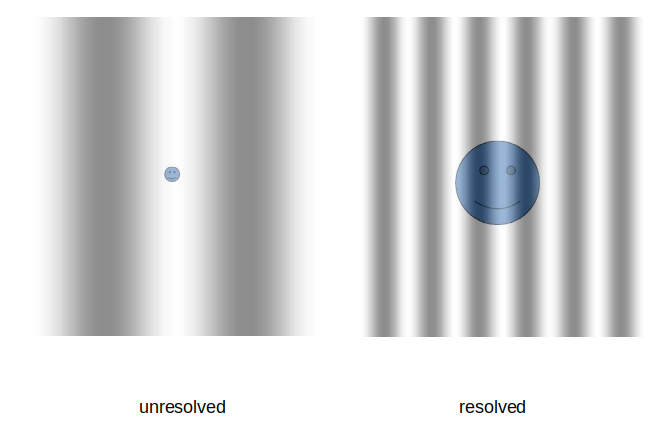
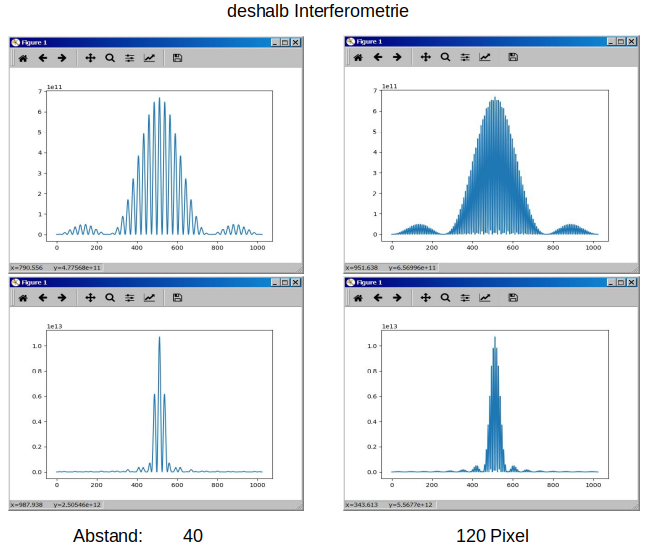
Im obigen Bild wurden in der oberen Zeile zwei schmale/kleine Spalte/Teleskope auseinander geschoben, in der unteren zwei große, auf dieselbe Distanz.
Unten ist es besser in Auflösung und Helligkeit (Amplitude).
Für das Auflösungsvermögen (theta) gilt
theta ~ lambda / D
lambda ist die benutzte Wellenlänge, D der Durchmesser des Teleskops, bzw. der entferntesten Teleskope beim Interferometer. Ist D groß, ist theta, der aufgelöste Winkel klein. Gilt genauso für kleines lambda. Deshalb arbeitet ALMA (anders als Effelsberg) auch im mm-Bereich und darunter.
Bei kürzeren Wellenlängen steigt natürlich auch die Anforderung an die Oberflächengenauigkeit der Schüsseln.
Das bisher mit Fernrohr und Spalt gesagte ist beim Radioteleskop bzw. beim Radiointerferometer nicht anders, es ist hier nur als Polardiagramm dargestellt.
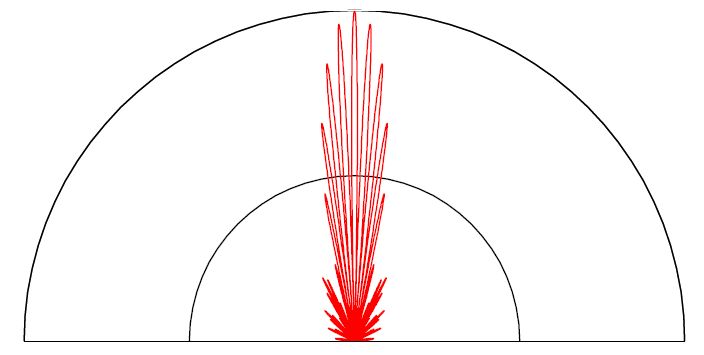
Wenn man nicht nur 2 Spalte (Teleskope) nimmt, sondern N>2, ergibt sich ein Gitter und die Auflösung steigt an (noch mehr rauf und runter).

Das Problem ist jetzt, dass wir ja ein Bild mit nur einem Pixel haben. Das ist absurd. Was tun ?
Na ja, wir statten das Teleskop mit Encodern aus, die uns stehts 2 Koordinaten (Winkel gegen die Nord-Richtung, Höhe über dem Horizont) zur gemessenen Intensität liefern. Zusätzlich merken wir uns die Zeit der einzelnen Messung.
Steht das Teleskop dabei still, dreht sich die Erde aber weiter (bzw. scheinbar der Himmel). Nachdem wir so etliche Messwerte aufgenommen haben, fahren wir das Gerät ein Stück zurück und etwas höher und lassen das Beobachtungsobjekt wie zuvor vorbeiziehen. So können wir Zeile für Zeile eine Karte (ein Bild aufbauen, scannen), etwa so wie früher beim Röhrenfernseher.
Wenn die Teleskope, so wie hier beim Westerborg Array, preußisch in eine Reihe stehen, sagen wir in x-Richtung, kann man in y natürlich keine Auflösung gewinnen, oder ?

Eigentlich ja, aber da ist ja noch die Erddrehung. Sie hilft den Radioastronomen gegen das Problem anzukämpfen. (schlaue Leute)
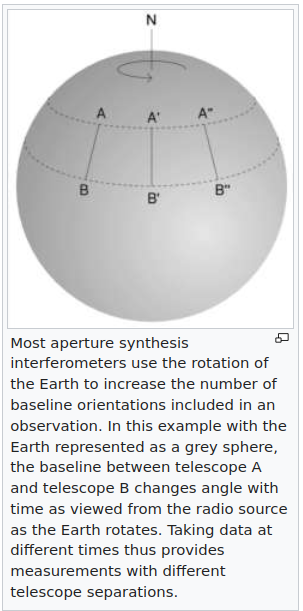
ALMA haben wir damit aber immer noch nicht.
Wie man im Bild oben sah, stehen die Teleskope da irgendwie wild in der Gegend rum. Was soll das? Die Idee dahinter geht so: ich wähle irgend eines der Dinger aus und ziehen zu jedem anderen eine gerade Linie, bilde so ein zweier-Interferometer mit dem jeweils anderen.
Das gibt aber ein ziemliches Chaos, oder?
Jein, mehr im zweiten Teil.
