Wie man mit ALMA Bilder macht – Teil 2

Leider geht es im Teil 2 nicht ohne Mathe. Wem das zu trocken ist, der überfliegt es und sieht sich die Filme am Ende an.

Die obige Folie hab ich aus dem Vortrag von David J. Wilner, Harvard-Smithsonian Center for Astrophysics entnommen (Link am Ende des Beitrags). Sie zeigt das wesentliche auf, was wir wissen müssen, um der Interferometrie mit Radioteleskopen näher zu kommen.

Gegeben: T(l,m) == Radioquelle am Himmel mit den Koordinaten l,m und zwei Radioteleskope, die unser Interferometer bilden. Eines liegt im Ursprung einer Ebene (Koordinaten u,v) deren Normalenvektor zur Quelle zeigt. Die Koordinaten der Teleskope, u,v werden in Wellenlängen angegeben.

Wenn es uns gelingt, mittels der Messwerte der Teleskope, V(u,v) zu konstruieren, läßt sich die Intensitätsverteilung T(l,m), das ist unser gesuchtes Bild, rekonstruieren. Die mathematische Operation, die wir dazu brauchen, ist eine zweidimensionale Fouriertransformation (siehe Bild oben). V(u,v) ist eine komplexe Funktion, die sogenannte Visibility.

Im Ursprung gilt: V(u=0,v=0) ist das Integral von  T(l,m)dldm = totaler Fluß.

Das Interferometer liefert als Meßwert, als Output des Korrelators zwei Größen, Rc und Rs, die als Komponenten einer komplexen Zahl V aufgefaßt werden. Deren Wert wird bei den Koordinaten u,v in der Ebene gespeichert. . Sie gehören somit zu den Koordinaten l,m am Himmel. Viele dieser Meßwerte füllen immer mehr Punkte unserer synthetisierten, riesigen Radioschüssel.

In Teil 1 hatten wir beim Doppelspalt gesehen, wie ein immer feineres cosinusförmiges Muster entsteht, wenn die Spalte auseinanderrücken.

 

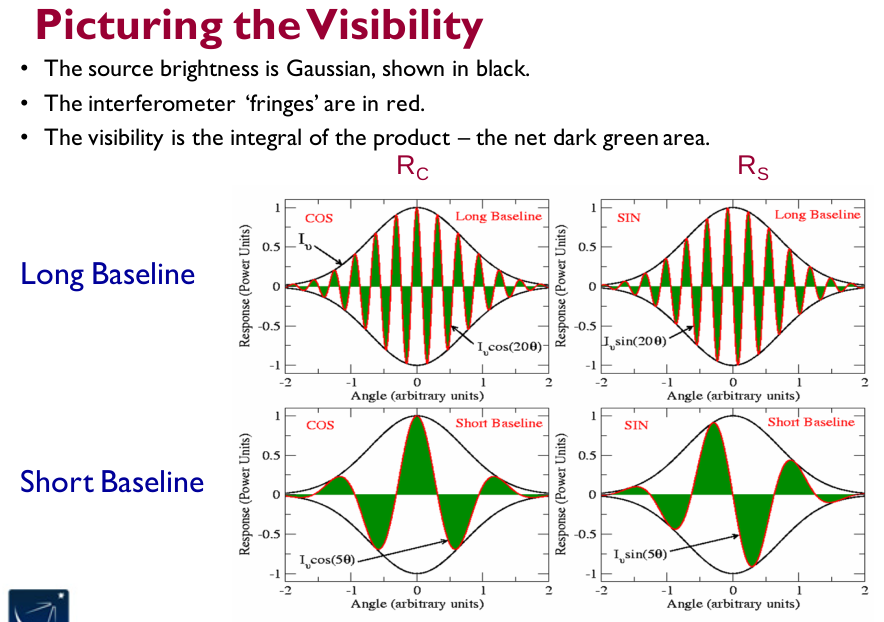
So ist es beim Interferometer auch. Es legt solch ein Wellenmuster über das Beobachtungsobjekt (Fringes, im obigen Bild ist die schwarze Kurve das Objekt.) Wir erhalten so einen Zusammenhang zwischen der Helligkeitsverteilung und der Fringe-Separation und Orientierung. Das Interforometer mißt die Summe (Integral) über das Produkt dieses Musters mit der Intensität der Quelle  bei den aktuellen Koordinaten (grüne Flächen).

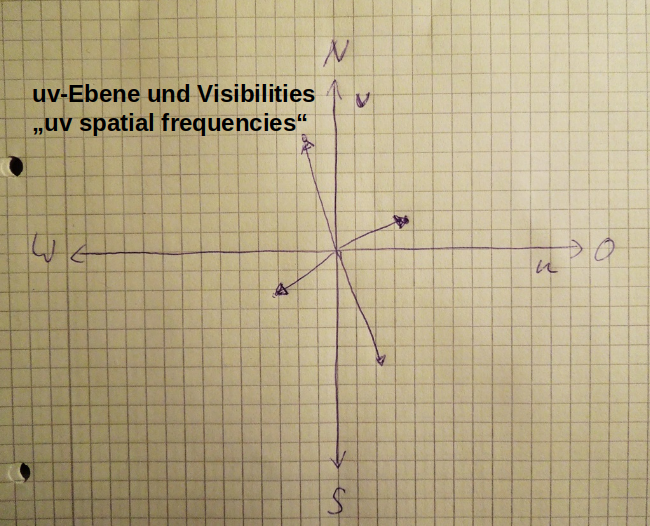
uv-Ebene zeigt Verbindung von Teleskop 1 im Ursprung, zu zwei weiteren Teleskopen. Meßwerte werden aus mathematischen Gründen auch am Ursprung gespiegelt eingetragen.

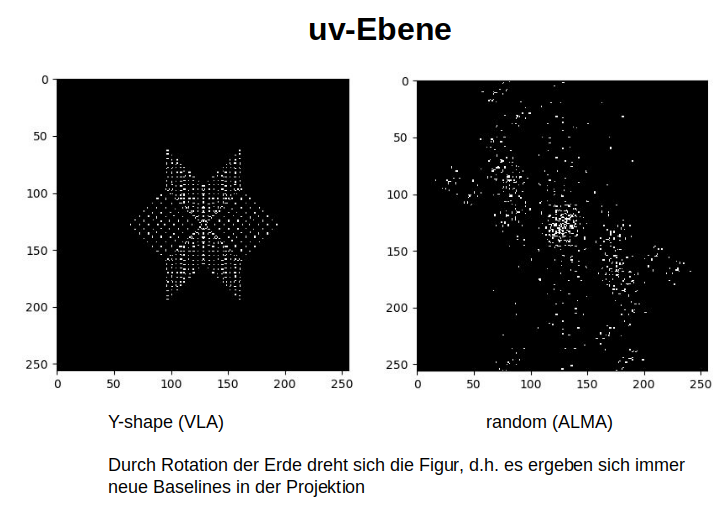
Lückenhaft gefüllte uv-Ebene. Auf der linken Seite mal für die  regelmäßige Y-Anordnung des VLA gezeigt, rechts die chaotische für ALMA.

 

APERTURE SYNTHESIS

Oben der Idealfall.

Im linken Bild wird die komplett weiße, synthetisierte “Teleskopöffnung” gezeigt ( für eine ebene Welle mit Wellenvektor senkrecht zur Öffnung).

Im rechten oberen Bild sehen wir das Beugungscheibchen. Es ergibt sich aus der 2 dimensionalen Fourier-Transformation des linken Bildes (Power-Spektrum, alles wie beim optischen Teleskop auch).

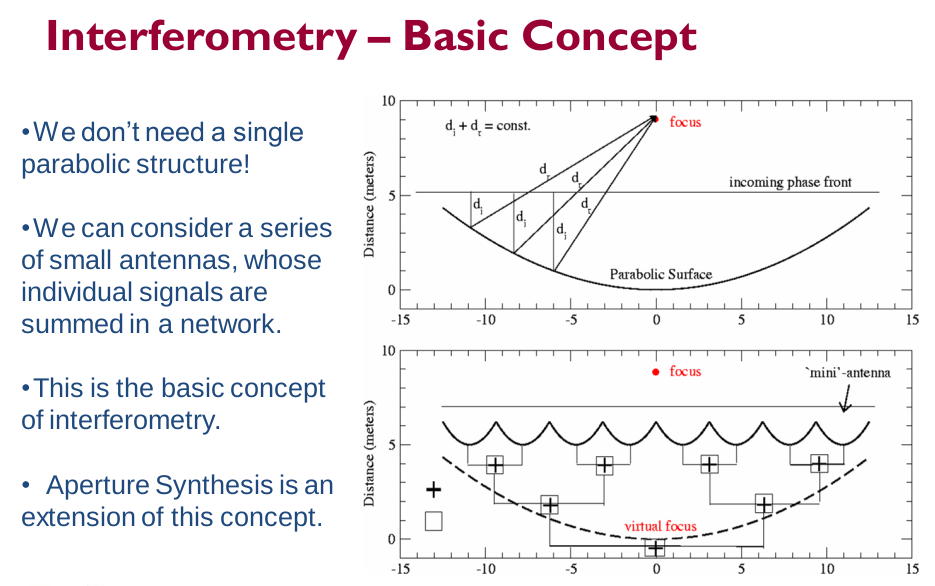
Im obigen Bild wird das oben gezeigte Paraboloid des Teleskops durch eine Serie von kleinen Schüsseln (unten) ersetzt. Bei gleichem Gesamtdurchmesser und gleicher Fläche ist es dann gleichwertig zu großen Teleskop, das man ja im Durchmesser von km gar nicht bauen könnte.

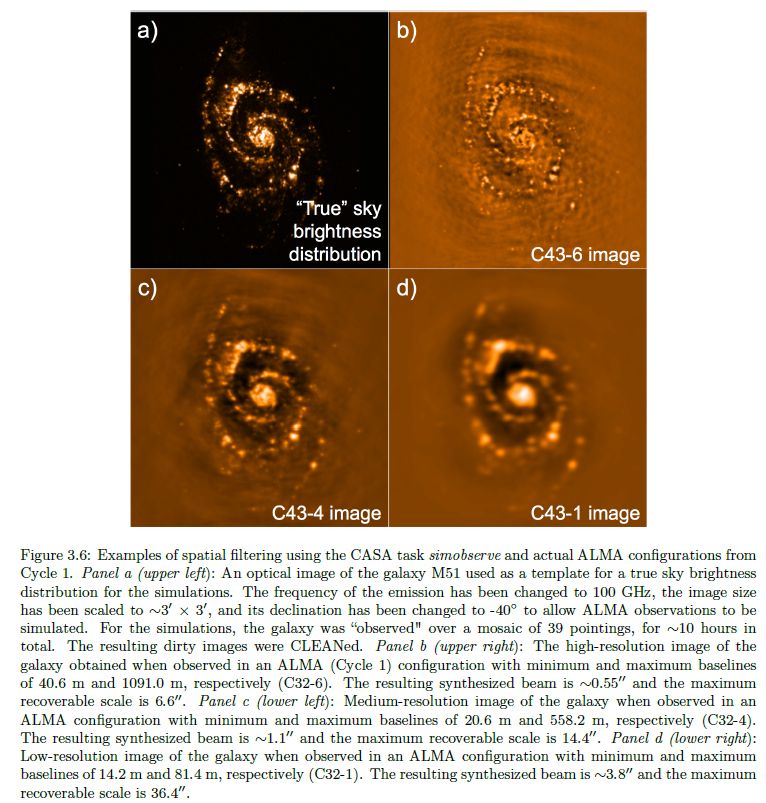
Was passiert, wenn man jetzt einige der kleinen Teleskope wegläßt (Lücken in der uv-Ebene) ? Zunächst nicht so viel, ähnlich wie bei eurem Spiegeteleskop, bei dem der Fangspiegel ja auch Licht aus der komplett erleuchteten Öffnung frißt. Dann aber sieht man es dem Ergebnis an:

Wir erhalten das sogenannte “dirty image” als Faltung des gesuchten idealen Bildes mit der unvollständigen PSF (dirty beam).  Man versucht jetzt eine Entfaltung (Deconvolution) der PSF aus dem dirty image um eine Modell für die Quelle zu erhalten… usw.

Bei ALMA können die 66 Teleskope nicht den weißen Kreis mit einem Durchmesser von bis zu 16 km nicht vollständig füllen, trotz Hilfe durch die Erddrehung, wie die folgenden Bilder der uv-Ebene zeigen.

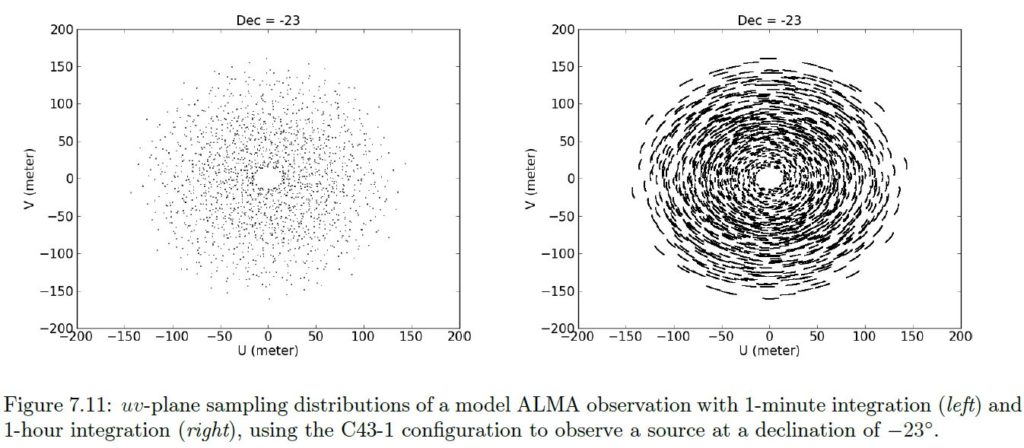
Im obigen Bild sieht man die uv-Ebene links nach 1-min Integrationszeit, rechts nach einer Stunde, wo die Erddrehung ihren Beitrag geleistet hat. Unten die daraus entstehenden  Bilder.

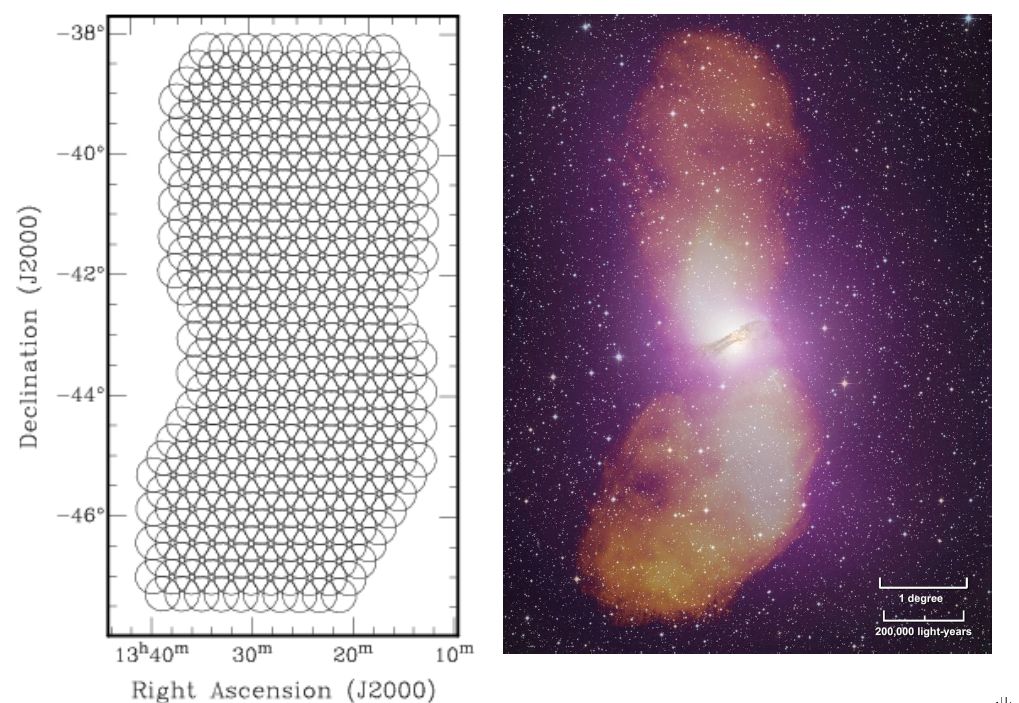
Im unteren Bild sieht man mal die Teleskop-Pointings die für das Bild rechts erforderlich waren.

Jetzt kommt nur noch pure Entspannung

 

100 t im Nacken, und das in 5000m Höhe!

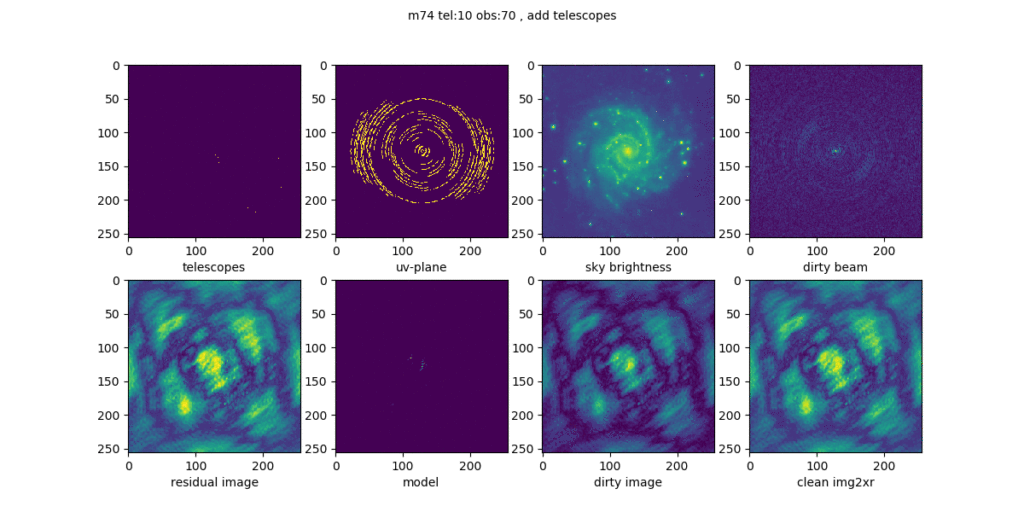
Die Videos (anklicken nicht vergessen)  zeigen den Einfluß der Messzeit auf die Aperture Sythese.

Es sind jeweils 8 Einzelbilder zu sehen. Ganz oben links ist jeweils die Verteilung der Teleskope gezeigt. In den ersten beiden Videos nimmt ihre Zahl von Schritt zu Schritt zu, um den Einfluß von mehr und mehr Teleskopen zu verdeutlichen.

Im zweiten Bild der oberen Reihe sieht man die jeweilige uv-Ebene und den Einfluß der Erddrehung.

Das dritte Bild ist das was am Himmel beobachtet wird, die Galaxie M74. Danach ist die Keule des Teleskops zu sehen.

Die untere Reihe zeigt Zwischenbilder bis auf das ganz rechte, welches das Endergebnis für die Konfiguration im jeweiligen Schritt zeigt.

 

Im obigen Video benutze ich eine weite Verteilung der Teleskope, was am Ende ein scharfes Bild unten rechts liefert.

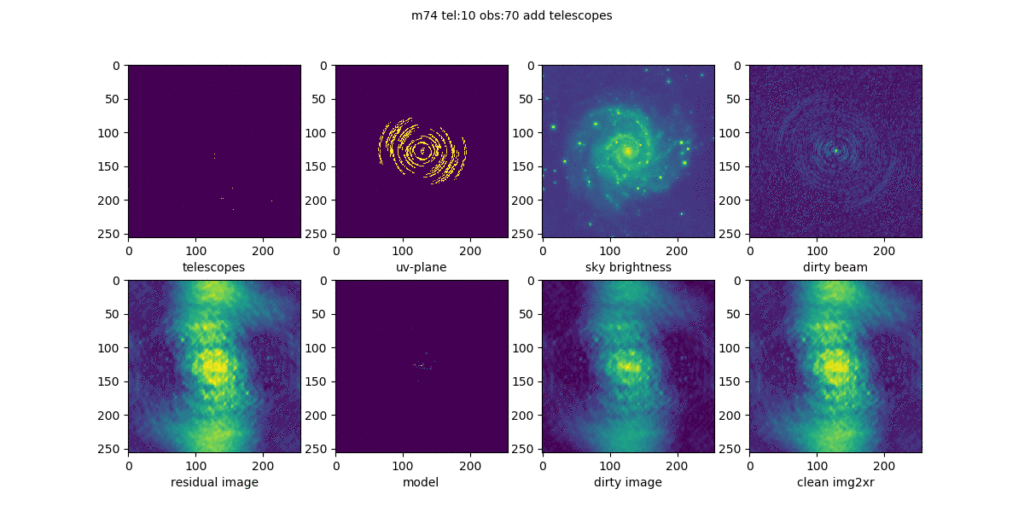
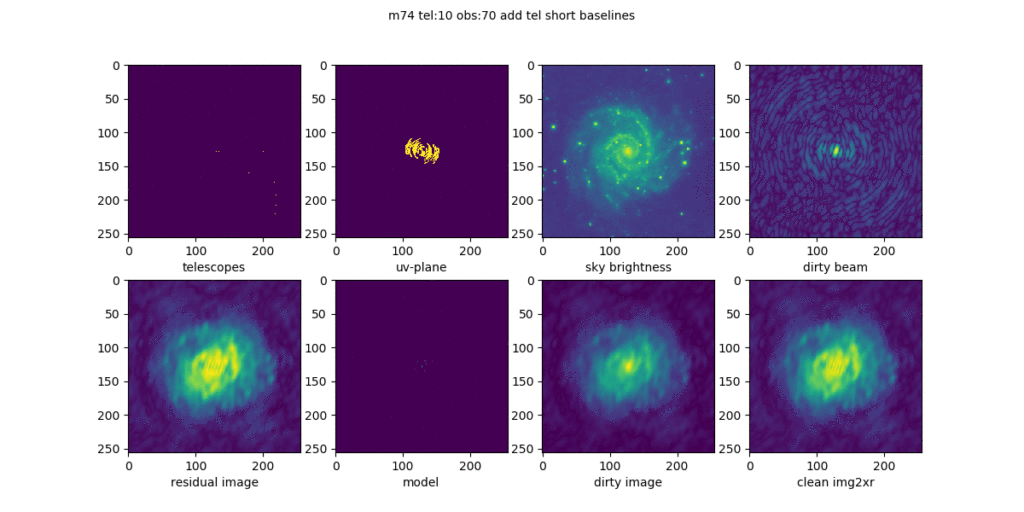
Im obigen Video stehen die Teleskope enger zusammen. Ergebnis Bild wird nicht so scharf. Wird im folgenden Bild noch deutlicher.

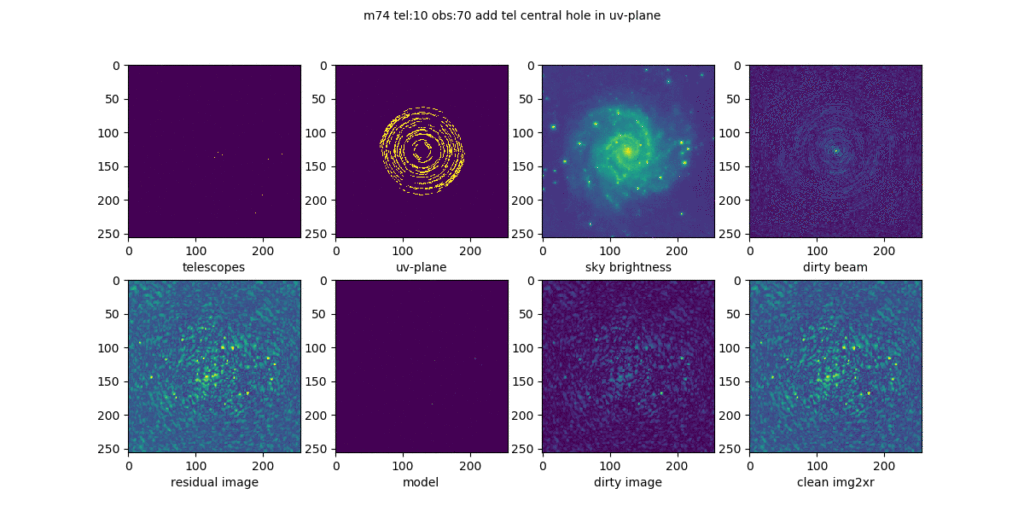
Im folgenden Video gibt es ein zentrales Loch in der uv-Ebene, also bei den ganz kurzen Baselines. Die Teleskopverteilung liefert so zwar ein scharfes Bild, aber dem fehlt die Helligkeit. Man kann die 12m-Schüsseln ja nicht beliebig nah zusammenschieben, um auch ganz kurze Baselines zu erzeugen. Deshalb gibt es bei Alma auch einige Teleskope mit 7m Durchmesser.

Programmiert hab ich den Simulator in Python und CUDA.

Nicht angesprochene Probleme

da gibt es eine lange Liste. Wir haben

nur das mono-chromatische Problem behandelt,
keine Polarisation,
keine zeitliche Variabilität der Quelle berücksichtigt,
die uv-Ebene ist eine idealisierte Vorstellung.  Eine dritte w-Komponente wird bei größeren Gesichtsfeldern und/oder unebenem Terrain, oder bei VLBI notwendig,
keine Atmosphäre (Wasserdampf), Ionosphäre berücksichtigt,
Ideale Elektronik (identisch für alle Antennen, kein Rauschen, perfekt lineares Verhalten, vorausgesetzt,
ebenso perfektes Pointing
keine Antennendeformationen, keine thermischen Gradienten, keine
Amplituden oder Phasenmuster,
keinen Wind, keinen Regen, keinen Schnee gehabt …
Bildverarbeitung „cleaning“ wurde nicht angesprochen.

Es gilt also wie immer:

Alles wäre nicht so schwer, wenn es etwas leichter wär.

Auch von Interesse im Zusammenhang.

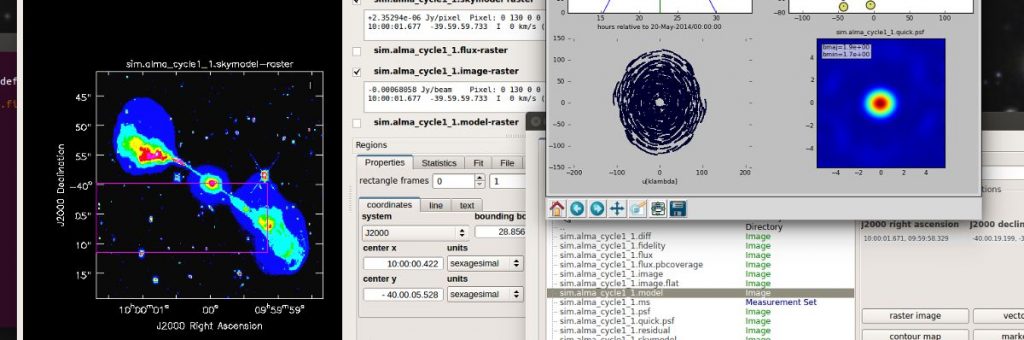
Wer mit Daten aus dem ALMA-Archiv experimentieren möchte, sollte sich die Casa-Software installieren. Würde mich freuen, wenn ihr mir interessante Ergebnisse zukommen laßt. Hier ein Screenshot:

 

Das alles und noch viel meeehr …

Könnt ihr hier nachlesen. Es is in Wirklichkeit noch viel komplizierter 🙁